Bernds Rappelkiste

Im Endeffekt lauten die Bedingungen wiefolgt:

für x <= 3 : y = 8
für x >= 8 : y = 5
Zwischenwerte 3 < x < 8 werden linear interpoliert

In der Grafik sieht die Funktion also so aus, dass man erstmal eine horizontale Linie bei y = 5 hat, dann fällt die Linie linear auf y = 5 ab und geht dann horizontal weiter.

Bereich 1 und 3 sind kein Problem, aus den vorherigen Beiträgen ist ja bereits bekannt, wie die einzelnen Linien gezeichnet werden können. Mein Problem, wenn man es so nennen will, ist der Bereich zwischen 3 < x < 8, für den man eine Geradengleichung benötigt. Ich hatte gehofft, dass Maxima dazu eine Funktion “Gerade durch zwei Punkte” bieten würde, aber leider habe ich nichts dazu gefunden. Falls jemand einen Tipp dafür hat, ich höre gerne zu

Da die Geradengleichung natürlich trotzdem benötigt wird, muss die gute alte Algebra aus der 7ten Klasse herhalten.

Zuerst einmal definiert man sich die zwei Punkte A und B der Gerade. Die Werte in den eckigen Klammern geben natürlich die x- und y-Koordinaten wieder. Danach werden die einzelnen Werte auf die Variablen x1, y1, x2 und y2 verteilt.

A  : [3,8];  B  : [8,5];
x1 : A[1];   y1 : A[2];
x2 : B[1];   y2 : B[2];

Als nächstes wird die allgemeine Geradengleichung definiert:

g(x,y) := y=k*x+d;

Nun kann man sich jeweils für A und B eine eigene Geradenfunktion erstellen lassen, in die die Werte von x und y eingesetzt werden:

g1 : g(x1,y1);
g2 : g(x2,y2);

Die beiden Gleichungen kann man nun gleichsetzen und nach den beiden Unbekannten k und d lösen lassen. Zwei Gleichungen mit zwei Unbekannten, das geh t

l : solve([g1, g2], [k, d]);

Nachdem man nun die Steigung und den Y-Achsenabschnitt der Geradengleichung kennt, kann man sich die endgültige Geradengleichung in eine Variable ausgeben lassen:

Gerade : k * x + d, l;

Das schwierigste ist geschafft, jetzt muss man sich nur noch abschnittsweise seine Funktion zusammenbauen. Die Bedingungen von oben kann man sich leicht umformen und mit etwas Englisch und logischem Verständnis in eine schöne IF-Bedingungen basteln:

f(x) := if x <= x1 then y1 else
        if x >= x2 then y2 else
        Gerade;

Als nächstes lassen wir uns zur Kontrolle mal alle Funktionen ausgeben, die wir definiert haben:

wxplot2d( [y1, y2, Gerade, f(x)], [x, 0, 10], [y, 0, 10]);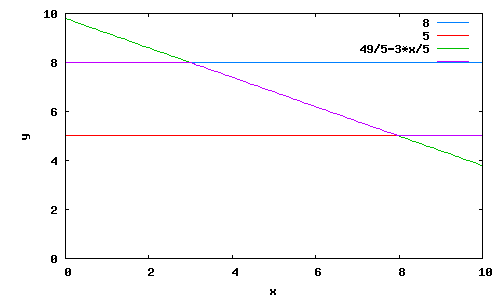

Das sieht doch ganz gut aus, also können wir auf die einzelnen Funktionen verzichten und nehmen uns nur unsere abschnittsweise heran:

wxplot2d( [f(x)], [x, 0, 10], [y, 0, 10]);

Und warum der Aufwand? Weil man sich jetzt einfach an jeder beliebigen Stelle von x den passenden Wert ausgeben lassen kann, ohne darauf achten zu müssen, in welchem Bereich man gerade ist